Cosmic Microwave Background

So this whole time we have been talking about how the theory of a Hot Big Bang is the most accepted theory in cosmology today, but it was not always that way. It finally started to gain popularity with the discovery and identification of the Cosmic Microwave Background. To begin, in the middle of the 20th century, George Gamow surmised that if matter had been created during decoupling, than the primordial radiation (ie. the photons that decoupled from the matter) should be present with an almost perfect uniformity everywhere in the universe. He inaccurately predicted the temperature of this radiation to be about 50 K (-267°C), but his students later re-calculated the temperature to be 5 K. However, there was still no empirical proof of the existence of the radiation, so Gamow's theory fell somewhat into obscurity.

Things started to heat up again in 1965 when Arno Penzias and Robert Wilson, radio astronomers working for Bell Laboratories, found a mysterious microwave signal causing background noise in their radio telescope. The strange part was that the signal seemed to come from everywhere. A group at Princeton was able to identify this radiation as the leftover remnants of the Big Bang, called the Cosmic Microwave Background, or CMB for short. The spectrum of the CMB fits that of a black body nearly perfectly, and so via the black body curve the temperature of the CMB has been determined to be about 2.7 K. Due to its near perfect uniformity, scientists conclude that this radiation originated in a time when the universe was much smaller, hotter, and denser. So as a result of the continual expansion of the universe, the light waves of this radiation have stretched out to longer wavelengths which today exist in the microwave region of the electromagnetic spectrum (which is why we call it the Cosmic "Microwave" Background).

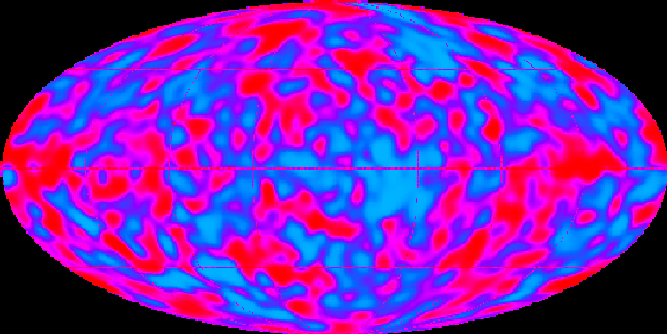
This is a picture of an anisotropy map taken by the Cosmic Microwave Background Explorer (COBE). (To get to the COBE homepage, click here.) The COBE satellite was sent up in 1989 search for temperature anisotropies in the Cosmic Microwave Background, frequently called the CMB.

You're probably asking yourself, "What in the @#*&%! does "anisotropy" mean? Well, when we say something is isotropic, that means it is uniform. We mentioned isotropy in our references to a steady state universe (ie having approximately the same makeup throughout). However, anisotropy means just the opposite: not uniform. Astronomers and physicists suspected that the Cosmic Microwave Background might display very slight fluctuations in temperature, but this data could not be accurately recorded until the flight of COBE because it was the first satellite experiment to gather information from outer space, where all of the background noise from water vapor could be eliminated. How does water vapor cause problems for detecting microwaves? Well, we mentioned before how your microwave will only cook foods that contain water. That is because water absorbs microwaves. That makes the microwaves very difficult to observe, especially when scientists are looking at temperature variations that are on the order of microKelvin (that's one one-millionth of a degree).

So what do the spots on the map mean?

The spots on the map correspond to photon energies at the time of the last scattering of photons by electrons. The areas of higher energy are blue, while the areas of low energy are red. If this is a little confusing, try to imagine the colors in a campfire. The hottest and most energetic part of the fire is the blue flame, while the red flame is the coldest and least energetic part of the fire. The same thing applies to this map of the CMB temperature anisotropies. The blue spots are hotter regions of more energy, and the red spots are colder regions of less energy. The strange thing is, the cold spots (ie. red spots) are the more dense regions. Why, you ask? Well, these cold regions are what we call gravitational potential wells, so the photons are "pulled" in these regions by gravity, making them more dense. Originally, these regions would be hotter then the less dense regions because when you compress a gas for example, the temperature increases as more particles collide with each other. However, it requires a lot of energy for the photons to overcome the gravitational pull and exit these potential wells, so these areas actually end up having less energy and are colder than the less dense regions.

Color Energy Temperature Density
red lowest coldest highest
magenta medium low medium cold medium high
blue medium high medium warm medium low
turquoise highest hottest lowest

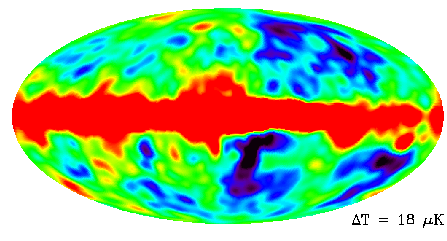
A Word of Caution...

Be careful when looking at these anisotropy maps! They can be very misleading. First of all, the temperature variations in the CMB are very, very small, and the CMB is uniform up to about 1 part in 100,000. So the variances in temperature have a range of 2.7K ± 0.00003. If you were to just look at the CMB, it would look entirely uniform, but scientists have enhanced these small perturbations in the CMB so that you can see them in the map.

Further, it is important to note that the microwave radiation that reaches us from our galaxy, the Milky Way, and the effect of the rotation of the Earth have been editted out. If the effect from th radiation from the Milky Way had been left in, for example, the map you see would have a huge band running straight through the middle of it like on the temperature map below.

This map shows temperature changes in the CMB where the effect of the Milky Way in the data has not been removed. The red spots are the hotter spots and the blue spots are colder. However, look at the scale of temperature changes. The delta t is equal to 18 microKelvin which means that a the difference between the average temperature and the temperature of a hot or cold spot is only 0.000018 K. That is really small!

Why do we study the CMB?

There are a lot of reasons to look at the Cosmic Microwave Background. We hope we can find the answers to how and why the galaxies formed, and how the universe expanded. We are especially interested in what we call the geometry, or shape, of our universe. To start, we all know from Newtonian Mechanics that things that have mass exert a gravitational force which is proportional to their mass (ie. the more mass something has, the more gravitational pull it exerts). For example, the Earth's gravity is what keeps us from falling off it. Moreover, the galaxies in our local group are actually moving toward each other due to gravity. The density of matter in our group is high enough to overcome the force of the expansion of our universe. On a larger scale, our universe also has a specific density of matter, but that is a very hard quantity to determine because we do not know just how big the universe is. Based on the rate of expansion of our universe, however, we can figure out what the critical density of our universe is. The "critical density" refers to the minimum density of the universe that would be needed to have enough "gravitational pull" to overcome the expansion of the universe and cause it to re-collapse. We define a parameter omega as the (actual density of the universe) / (critical density). If omega is greater than 1, we say the universe has a positive curvature and call this scenario a closed universe because eventually gravity will overcome the expansion and cause the universe to re-collapse. On the other hand, if omega is less than 1, then the universe will expand forever; we call this an open universe with a negative curvature. The last scenario is when omega is equal to 1 because the force of gravity is exactly enough to counter the force of the expansion, and so the universe will continue to expand, but it's rate of expansion will slow down asymptotically to 0; we call this a flat universe.

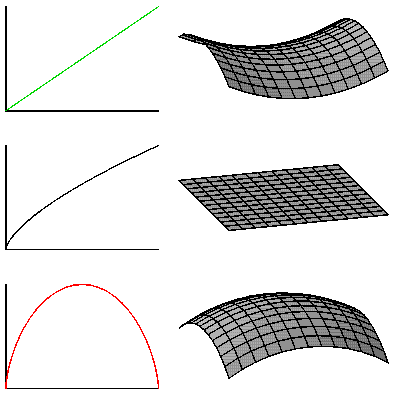
If this is confusing, think of it like throwing a baseball straight up into the air. Let's say the rate of expansion is the initial velocity of the ball, which depends on how hard you throw it. Earth's gravity will act on the ball and cause it to slow down. Three things could happen. First, the ball may eventually slow to a stop and fall back to Earth, accelerating downward as it falls (like a closed universe), or the ball will start to slow down, but still be moving just enough so that the speed of the ball slows asymptotically to 0 (like a flat universe), or if you can throw the ball hard enough, the ball will slow down but still have enough energy to escape the force of the Earth's gravity (escape velocity) and will just continue to travel away from the Earth at a constant speed (like an open universe). So, by studying the CMB, scientists have been able to put bounds on the possible values for omega and know now that omega is equal to 1, which means our universe is flat.

(Picture courtesy of Ned Wright's Cosmology Tutorial)

Open Universe:

omega < 1 and the universe has a negative curvature

Flat Universe:

omega = 1 and the universe has Euclidean geometry

Closed Universe:

omega > 1 and the universe has a positive curvature

More than meets the eye...

Well, let's just say that sometimes things are more complicated than they seem. In the early 20th century, Albert Einstein proposed a term in his equations for General Relativity that he called the Cosmological Constant. He later referred to it as "the greatest mistake of his life," but recent observations of Type 1a Supernovae have shown that the notion of a cosmological constant may not be a "mistake" after all. For a long time people just assumed it was 0 (which was just such the case in our previous paragraph), but current cosmological models seem to imply that it is non-zero. This means that the value of omega-total also depends on this parameter which we call omega-lamda. All this basically says is: just because we say the universe is flat does not mean we know what its destiny is (hmmm, this seems to contradict everything from the first paragraph). Inevitably, scientists find themselves completely baffled once again with the complexities of our universe, and the search is still on for the key to unlock the door to its greatest mysteries.

Return to top.

Home | Introduction | Brief History | Olbers' Paradox | Hubble Expansion | Big Bang Theory | Electromagnetic Spectrum | CMB | Glossary of Terms